Measurement-induced entanglement and teleportation on a loud quantum processor

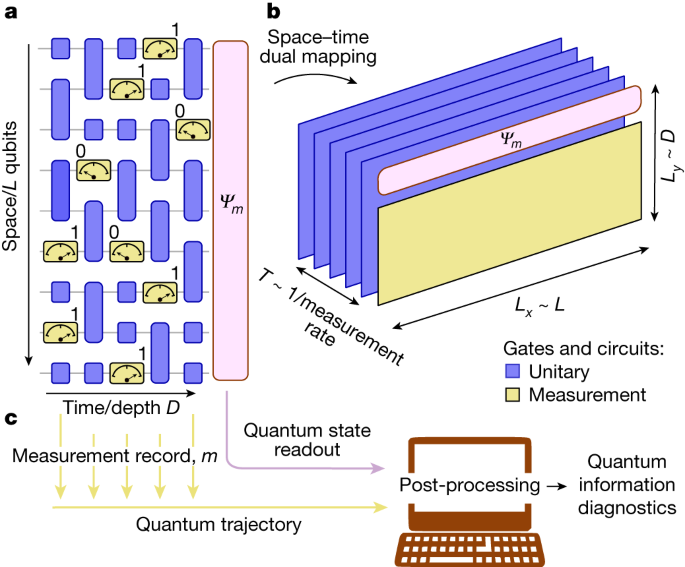
The stochastic, non-unitary nature of measurement is a foundational precept in quantum concept and stands in stark distinction to the deterministic, unitary evolution prescribed by Schrödinger’s equation¹. Due to these distinctive properties, measurement is vital to some basic protocols in quantum data science, comparable to teleportation², error correction¹⁹ and measurement-based computation²⁰. All these protocols use quantum measurements, and classical processing of their outcomes, to construct explicit buildings of quantum data in area–time. Remarkably, such buildings can also emerge spontaneously from random sequences of unitary interactions and measurements. Particularly, ‘monitored’ circuits, comprising each unitary gates and managed projective measurements (Fig. 1a), had been predicted to present rise to distinct non-equilibrium phases characterised by the construction of their entanglement^3,4,21,22,23, both ‘quantity legislation’²⁴ (in depth) or ‘space legislation’²⁵ (restricted), relying on the speed or power of measurement.

a, A random (1 + 1)-dimensional monitored quantum circuit composed of each unitary gates and measurements. b, An equal twin (1 + 1)-dimensional shallow circuit of measurement L_x × L_y and depth T with all measurements on the ultimate time fashioned from an area–time duality mapping of the circuit in a. Due to the non-unitarity nature of measurements, there may be freedom as to which dimensions are seen as ‘time’ and which as ‘area’. On this instance, L_y is ready by the (1 + 1)D circuit depth and L_x by its spatial measurement, and T is ready by the measurement fee. c, Classical post-processing on a pc of the measurement document (quantum trajectory), and quantum-state readout of a monitored circuit can be utilized to diagnose the underlying data buildings within the system.

In precept, quantum processors enable full management of each unitary evolution and projective measurements (Fig. 1a). Nevertheless, regardless of their significance in quantum data science, the experimental examine of measurement-induced entanglement phenomena^26,27 has been restricted to small system sizes or effectively simulatable Clifford gates. The stochastic nature of measurement signifies that the detection of such phenomena requires both the exponentially expensive post-selection of measurement outcomes or extra refined data-processing strategies. It’s because the phenomena are seen solely within the properties of quantum trajectories; a naive averaging of experimental repetitions incoherently mixes trajectories with totally different measurement outcomes and totally washes out the non-trivial physics. Moreover, implementing the mannequin in Fig. 1a requires mid-circuit measurements which might be typically problematic on superconducting processors as a result of the time wanted to carry out a measurement is a a lot bigger fraction of the everyday coherence time than it’s for two-qubit unitary operations. Right here we use area–time duality mappings to keep away from mid-circuit measurements, and we develop a diagnostic of the phases on the premise of a hybrid quantum-classical order parameter (just like the cross-entropy benchmark in ref. ²⁸) to beat the issue of post-selection. The steadiness of those quantum data phases to noise is a matter of sensible significance. Though comparatively little is understood concerning the impact of noise on monitored programs^29,30,31, noise is usually anticipated to destabilize measurement-induced non-equilibrium phases. Nonetheless, we present that noise serves as an impartial probe of the phases at accessible system sizes. Leveraging these insights permits us to comprehend and diagnose measurement-induced phases of quantum data on system sizes of as much as 70 qubits.

The area–time duality strategy^9,15,16,17 allows more-experimentally handy implementations of monitored circuits by leveraging the absence of causality in such dynamics. When conditioning on measurement outcomes, the arrow of time loses its distinctive position and turns into interchangeable with spatial dimensions, giving rise to a community of quantum data in area–time³² that may be analysed in a number of methods. For instance, we will map one-dimensional (1D) monitored circuits (Fig. 1a) to 2D shallow unitary circuits with measurements solely on the ultimate step¹⁷ (Fig. 1b and Supplementary Info part 5), thereby addressing the experimental challenge of mid-circuit measurement.

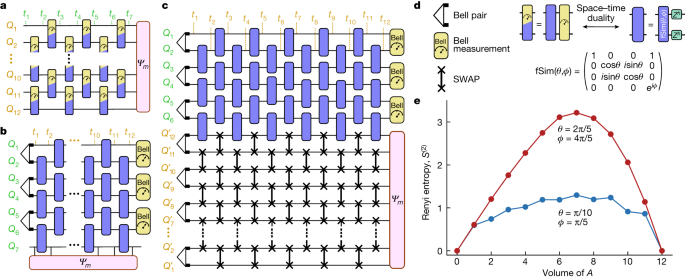
We started by specializing in a particular class of 1D monitored circuits that may be mapped by area–time duality to 1D unitary circuits. These fashions are theoretically nicely understood^15,16 and are handy to implement experimentally. For households of operations which might be twin to unitary gates (Supplementary Info), the usual mannequin of monitored dynamics^3,4 based mostly on a brickwork circuit of unitary gates and measurements (Fig. 2a) will be equivalently carried out as a unitary circuit when the area and time instructions are exchanged (Fig. 2b), leaving measurements solely on the finish. The specified output state |Ψ_m⟩ is ready on a temporal subsystem (in a set place at totally different instances)³³. It may be accessed with out mid-circuit measurements through the use of ancillary qubits initialized in Bell pairs (({Q}_{1}^{{prime} }ldots {Q}_{12}^{{prime} }) in Fig. 2c) and SWAP gates, which teleport |Ψ_m⟩ to the ancillary qubits on the finish of the circuit (Fig. 2c). The ensuing circuit nonetheless options post-selected measurements however their decreased quantity (relative to a generic mannequin; Fig. 2a) makes it potential to acquire the entropy of bigger programs, as much as all 12 qubits (({Q}_{1}^{{prime} }ldots {Q}_{12}^{{prime} })), in particular person quantum trajectories.

a, A quantum circuit composed of non-unitary two-qubit operations in a brickwork sample on a series of 12 qubits with 7 time steps. Every two-qubit operation generally is a mixture of unitary operations and measurement. b, The area–time twin of the circuit proven in a with the roles of area and time interchanged. The 12-qubit wavefunction |Ψ_m⟩ is temporally prolonged alongside Q₇. c, Within the experiment on a quantum processor, a set of 12 ancillary qubits ({Q}_{1}^{{prime} }ldots {Q}_{12}^{{prime} }) and a community of SWAP gates are used to teleport |Ψ_m⟩ to the ancillary qubits. d, Illustration of the two-qubit gate composed of an fSim unitary and random Z rotations with its area–time twin, which consists of a mix of unitary and measurement operations. The ability h of the Z rotation is random for each qubit and periodic with every cycle of the circuit. e, Second Renyi entropy as a operate of the amount of a subsystem A from randomized measurements and post-selection on Q₁…Q₆. The info proven are noise mitigated by subtracting an entropy density matching the whole system entropy. See the Supplementary Info for justification.

Earlier research^15,16 predicted distinct entanglement phases for |Ψ_m⟩ as a operate of the selection of unitary gates within the twin circuit: volume-law entanglement if the gates induce an ergodic evolution, and logarithmic entanglement in the event that they induce a localized evolution. We carried out unitary circuits which might be consultant of the 2 regimes, constructed from two-qubit fermionic simulation (fSim) unitary gates³⁴ with swap angle θ and section angle ϕ = 2θ, adopted by random single-qubit Z rotations. We selected angles θ = 2π/5 and θ = π/10 as a result of these are twin to non-unitary operations with totally different measurement strengths (Fig. 2nd and Supplementary Info).

To measure the second Renyi entropy for qubits composing |Ψ_m⟩, randomized measurements^35,36 are carried out on ({Q}_{1}^{{prime} }ldots {Q}_{12}^{{prime} }). Determine 2e reveals the entanglement entropy as a operate of subsystem measurement. The primary gate set provides rise to a Web page-like curve²⁴, with entanglement entropy rising linearly with subsystem measurement as much as half the system after which ramping down. The second gate set, against this, reveals a weak, sublinear dependence of entanglement with subsystem measurement. These findings are in step with the theoretical expectation of distinct entanglement phases (volume-law and logarithmic, respectively) in monitored circuits which might be area–time twin to ergodic and localized unitary circuits^15,16. A section transition between the 2 will be achieved by tuning the (θ, ϕ) fSim gate angles.

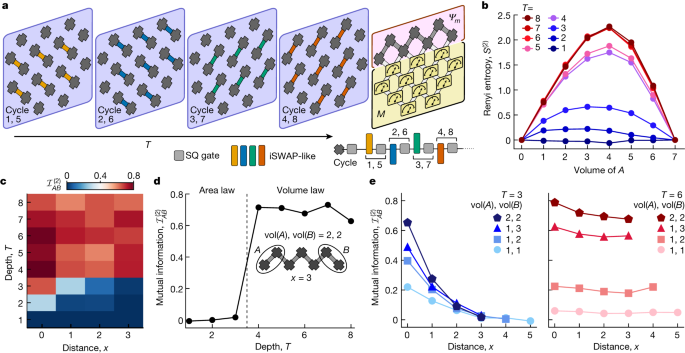
We subsequent moved past this particular class of circuits with operations restricted to be twin to unitary gates, and as a substitute investigated quantum data buildings arising underneath extra common circumstances. Generic monitored circuits in 1D will be mapped onto shallow circuits in 2D, with ultimate measurements on all however a 1D subsystem¹⁷. The efficient measurement fee, p, is ready by the depth of the shallow circuit, T, and the variety of measured qubits, M. Heuristically, p = M/(M + L)T (the variety of measurements per unitary gate), the place L is the size of the chain of unmeasured qubits internet hosting the ultimate state for which the entanglement construction is being investigated. Thus, for big M, a measurement-induced transition will be tuned by various T. We ran 2D random quantum circuits²⁸ composed of iSWAP-like and random single-qubit rotation unitaries on a grid of 19 qubits (Fig. 3a), with T various from 1 to eight. For every depth, we post-selected on measurement outcomes of M = 12 qubits and left behind a 1D chain of L = 7 qubits; the entanglement entropy was then measured for contiguous subsystems A through the use of randomized measurements. We noticed two distinct behaviours over a variety of T values (Fig. 3b). For T < 4, the entropy scaling is subextensive with the scale of the subsystem, whereas for T ≥ 4, we observe an roughly linear scaling.

a, Schematic of the 2D grid of qubits. At every cycle (blue containers) of the circuit, random single-qubit and two-qubit iSWAP-like gates are utilized to every qubit within the cycle sequence proven. The random single-qubit gate (SQ, gray) is chosen randomly from the set ({sqrt{{X}^{pm 1}},sqrt{{Y}^{pm 1}},sqrt{{W}^{pm 1}},sqrt{{V}^{pm 1}}}), the place (W=(X+Y)/sqrt{2}) and (V=(X-Y)/sqrt{2}). On the finish of the circuit, the decrease M = 12 qubits are measured and post-selected on probably the most possible bitstring. b, Second Renyi entropy of contiguous subsystems A of the L = 7 edge qubits at varied depths. The measurement is noise mitigated in the identical manner as in Fig. 2. c, Second Renyi mutual data ({{mathcal{I}}}_{AB}^{(2)}) between two-qubit subsystems A and B in opposition to depth T and distance x (the variety of qubits between A and B). d, ({{mathcal{I}}}_{AB}^{(2)}) as a operate of T for two-qubit subsystems A and B at most separation. e, ({{mathcal{I}}}_{AB}^{(2)}) versus x for T = 3 and T = 6 for various volumes of A and B.

The spatial construction of quantum data will be additional characterised by its signatures in correlations between disjointed subsystems of qubits: within the area-law section, entanglement decays quickly with distance³⁷, whereas in a volume-law section, sufficiently giant subsystems could also be entangled arbitrarily distant. We studied the second Renyi mutual data

between two subsystems A and B as a operate of depth T, and the gap (the variety of qubits) x between them (Fig. 3c). For maximally separated subsystems A and B of two qubits every, ({{mathcal{I}}}_{AB}^{(2)}) stays finite for T ≥ 4, nevertheless it decays to 0 for T ≤ 3 (Fig. 3d). We additionally plotted ({{mathcal{I}}}_{AB}^{(2)}) for subsystems A and B with totally different sizes (T = 3 and T = 6) as a operate of x (Fig. 3e). For T = 3 we noticed a fast decay of ({{mathcal{I}}}_{AB}^{(2)}) with x, indicating that solely close by qubits share data. For T = 6, nevertheless, ({{mathcal{I}}}_{AB}^{(2)}) doesn’t decay with distance.

The noticed buildings of entanglement and mutual data present sturdy proof for the belief of measurement-induced area-law (‘disentangling’) and volume-law (‘entangling’) phases. Our outcomes point out that there’s a section transition at important depth T ≃ 4, which is in step with earlier numerical research of comparable fashions^17,18,38. The identical evaluation with out post-selection on the M qubits (Supplementary Info) reveals vanishingly small mutual data, indicating that long-ranged correlations are induced by the measurements.

The approaches we’ve adopted to this point are troublesome to scale for system sizes better than 10–20 qubits²⁷, owing to the exponentially rising sampling complexity of post-selecting measurement outcomes and acquiring entanglement entropy of intensive subsystems of the specified output states. Extra scalable approaches have been not too long ago proposed^39,40,41,42 and carried out in effectively simulatable (Clifford) fashions²⁶. The important thing thought is that diagnostics of the entanglement construction should make use of each the readout information from the quantum state |Ψ_m⟩ and the classical measurement document m in a classical post-processing step (Fig. 1c). Put up-selection is the conceptually easiest occasion of this concept: whether or not quantum readout information are accepted or rejected is conditional on m. Nevertheless, as a result of every occasion of the experiment returns a random quantum trajectory⁴³ from 2^M potentialities (the place M is the variety of measurements), this strategy incurs an exponential sampling price that limits it to small system sizes. Overcoming this drawback will in the end require more-sample-efficient methods that use classical simulation^39,40,42, probably adopted by lively suggestions³⁹.

Right here we’ve developed a decoding protocol that correlates quantum readout and the measurement document to construct a hybrid quantum–classical order parameter for the phases that’s relevant to generic circuits and doesn’t require lively suggestions on the quantum processor. A key thought is that the entanglement of a single ‘probe’ qubit, conditioned on measurement outcomes, can function a proxy for the entanglement section of your entire system³⁹. This instantly eliminates one of many scalability issues: measuring the entropy of intensive subsystems. The opposite drawback—post-selection—is eliminated by a classical simulation step that permits us to utilize all of the experimental pictures and is due to this fact pattern environment friendly.

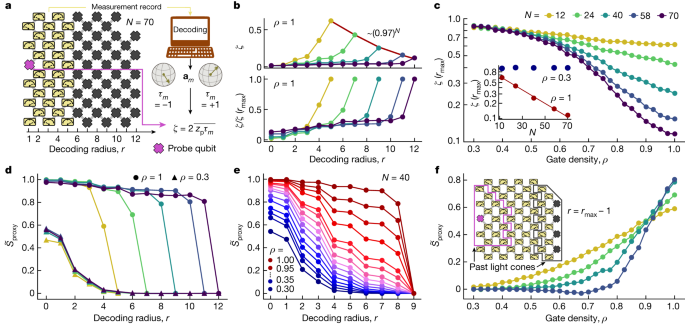
This protocol is illustrated in Fig. 4a. Every run of the circuit terminates with measurements that return binary outcomes ±1 for the probe qubit, z_p, and the encompassing M qubits, m. The probe qubit is on the identical footing as all of the others and is chosen on the post-processing stage. For every run, we classically compute the Bloch vector of the probe qubit, conditional on the measurement document m, a_m (Supplementary Info). We then outline ({tau }_{m}={mathsf{s}}{mathsf{i}}{mathsf{g}}{mathsf{n}}({{bf{a}}}_{m}cdot hat{z})), which is +1 if a_m factors above the equator of the Bloch sphere, and −1 in any other case. The cross-correlator between z_p and τ_m, averaged over many runs of the experiment such that the course of a_m is randomized, yields an estimate of the size of the Bloch vector, (zeta simeq overline{| {{bf{a}}}_{m}| }), which may in flip be used to outline a proxy for the probe’s entropy:

the place the overline denotes averaging over all of the experimental pictures and random circuit cases. A maximally entangled probe corresponds to ζ = 0.

a, Schematic of the processor geometry and decoding process. The gate sequence is similar as in Fig. 3 with depth T = 5. The decoding process includes classically computing the Bloch vector a_m of the probe qubit (pink) conditional on the experimental measurement document m (yellow). The order parameter ζ is calculated by the use of the cross-correlation between the measured probe bit z_p and ({tau }_{m}={mathsf{s}}{mathsf{i}}{mathsf{g}}{mathsf{n}}({{bf{a}}}_{m}cdot hat{z})), which is +1 if a_m factors above the equator of the Bloch sphere and −1 if it factors beneath. b, Decoded order parameter ζ and error-mitigated order parameter (widetilde{zeta }=zeta /zeta ({r}_{max })) as a operate of the decoding radius r for various N and ρ = 1. c, (zeta ({r}_{max })) as a operate of the gate density ρ for various N. The inset reveals that for small ρ, ζ(r_max) stays fixed as a operate of N (disentangling section), whereas for bigger ρ, ζ(r_max) decays exponentially with N, implying sensitivity to noise of arbitrarily distant qubits (entangling section). d, Error-mitigated proxy entropy ({widetilde{S}}_{{rm{proxy}}}) as a operate of the decoding radius for ρ = 0.3 (triangles) and ρ = 1 (circles). Within the disentangling section, ({widetilde{S}}_{{rm{proxy}}}) decays quickly to 0, impartial of the system measurement. Within the entangling section, ({widetilde{S}}_{{rm{proxy}}}) stays giant and finite as much as r_max − 1. e, ({widetilde{S}}_{{rm{proxy}}}) at N = 40 as a operate of r for various ρ, revealing a crossover between the entangling and disentangling phases for intermediate ρ. f, ({widetilde{S}}_{{rm{proxy}}}) at r = r_max − 1 as a operate of ρ for N = 12, 24, 40 and 58 qubits. The curves for various sizes roughly cross at ρ_c ≈ 0.9. Inset, schematic exhibiting the decoding geometry for the experiment. The pink and gray traces embody the previous gentle cones (at depth T = 5) of the probe qubit and traced-out qubits at r = r_max − 1, respectively. Knowledge had been collected from 2,000 random circuit cases and 1,000 pictures every for each worth of N and ρ.

In the usual teleportation protocol², a correcting operation conditional on the measurement final result have to be utilized to retrieve the teleported state. In our decoding protocol, τ_m has the position of the correcting operation, restricted to a classical bit-flip, and the cross-correlator describes the teleportation constancy. Within the circuits related to our experiment (depth T = 5 on N ≤ 70 qubits), the classical simulation for decoding is tractable. For arbitrarily giant circuits, nevertheless, the existence of environment friendly decoders stays an open drawback^39,41,44. Approximate decoders that work effectively in solely a part of the section diagram, or for particular fashions, additionally exist³⁹, and we’ve carried out one such instance  based mostly on matrix product states (Supplementary Info).

We utilized this decoding methodology to 2D shallow circuits that act on varied subsets of a 70-qubit processor, consisting of N = 12, 24, 40, 58 and 70 qubits in roughly sq. geometries (Supplementary Info). We selected a qubit close to the center of 1 facet because the probe and computed the order parameter ζ by decoding measurement outcomes as much as r lattice steps away from that facet whereas tracing out all of the others (Fig. 4a). We discuss with r because the decoding radius. Due to the measurements, the probe could stay entangled even when r extends previous its unitary gentle cone, akin to an emergent type of teleportation¹⁸.

As seen in Fig. 3, the entanglement transition happens as a operate of depth T, with a important depth 3 < T_c < 4. As a result of T is a discrete parameter, it can’t be tuned to finely resolve the transition. To do that, we repair T = 5 and as a substitute tune the density of the gates, so every iSWAP-like gate acts with chance ρ and is skipped in any other case, setting an ‘efficient depth’ T_eff = ρT; this may be tuned constantly throughout the transition. Outcomes for ζ(r) at ρ = 1 (Fig. 4b) reveal a decay with system measurement N of ζ(r_max), the place r  = r_max corresponds to measuring all of the qubits other than the probe. This decay is solely resulting from noise within the system.

Remarkably, sensitivity to noise can itself function an order parameter for the section. Within the disentangling section, the probe is affected by noise solely inside a finite correlation size, whereas within the entangling section it turns into delicate to noise wherever within the system. In Fig. 4c, ζ(r_max) is proven as a operate of ρ for a number of N values, indicating a transition at a important gate density ρ_c of round 0.6–0.8. At ρ = 0.3, which is nicely beneath the transition, ζ(r_max) stays fixed as N will increase (inset in Fig. 4c). In contrast, at ρ = 1 we match ζ(r_max) at round 0.97^N, indicating an error fee of round 3% per qubit for your entire sequence. That is roughly in step with our expectations for a depth T = 5 circuit based mostly on particular person gate and measurement error charges (Supplementary Info). This response to noise is analogous to the susceptibility of magnetic phases to a symmetry-breaking discipline^7,30,31,45 and due to this fact sharply distinguishes the phases solely within the restrict of infinitesimal noise. For finite noise, we anticipate the N dependence to be reduce off at a finite correlation size. We don’t see the results of this cut-off at system sizes accessible to our experiment.

As a complementary strategy, the underlying behaviour within the absence of noise could also be estimated by noise mitigation. To do that, we outline the normalized order parameter (widetilde{zeta }(r)=zeta (r)/zeta ({r}_{max })) and proxy entropy ({widetilde{S}}_{{rm{proxy}}}(r)=-{log }_{2}[(1+widetilde{zeta }{(r)}^{2})/2]). The persistence of entanglement with rising r, akin to measurement-induced teleportation¹⁸, signifies the entangling section. Determine 4d reveals the noise-mitigated entropy for ρ = 0.3 and ρ = 1, revealing a fast, N-independent decay within the former and a plateau as much as r = r_max − 1 within the latter. At mounted N = 40, ({widetilde{S}}_{{rm{proxy}}}(r)) shows a crossover between the 2 behaviours for intermediate ρ (Fig. 4e).

To resolve this crossover extra clearly, we present ({widetilde{S}}_{{rm{proxy}}}({r}_{max }-1)) as a operate of ρ for N = 12–58 (Fig. 4e). The accessible system sizes roughly cross at ρ_c ≈ 0.9. There may be an upward drift of the crossing factors with rising N, confirming the anticipated instability of the phases to noise within the infinite-system restrict. Nonetheless, the signatures of the best finite-size crossing (estimated to be ρ_c ≃ 0.72 from the noiseless classical simulation; Supplementary Info) stay recognizable on the sizes and noise charges accessible in our experiment, though they’re moved to bigger ρ_c. A secure finite-size crossing would imply that the probe qubit stays robustly entangled with qubits on the alternative facet of the system, even when N will increase. It is a hallmark of the teleporting section¹⁸, during which quantum data (aided by classical communication) travels sooner than the boundaries imposed by the locality and causality of unitary dynamics. Certainly, with out measurements, the probe qubit and the remaining unmeasured qubits are causally disconnected, with non-overlapping previous gentle cones⁴⁶ (pink and gray traces within the inset in Fig. 4f).

Our work focuses on the essence of measurement-induced phases: the emergence of distinct quantum data buildings in area–time. We used area–time duality mappings to bypass mid-circuit measurements, devised scalable decoding schemes based mostly on an area probe of entanglement, and used {hardware} noise to check these phases on as much as 70 superconducting qubits. Our findings spotlight the sensible limitations of NISQ processors imposed by finite coherence. By figuring out exponential suppression of the decoded sign within the variety of qubits, our outcomes point out that rising the scale of qubit arrays might not be helpful with out corresponding reductions in noise charges. At present error charges, extrapolation of our outcomes (at ρ = 1, T = 5) to an N-qubit constancy of lower than 1% signifies that arrays of greater than round 150 qubits would turn into too entangled with their atmosphere for any signatures of the best (closed system) entanglement construction to be detectable in experiments. This means that there’s an higher restrict on qubit array sizes of about 12 × 12 for one of these experiment, past which enhancements in system coherence are wanted.